Anirudh Rayabharam's personal blog

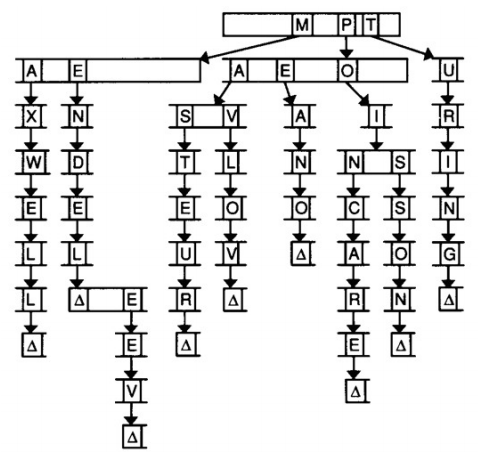
In the last week's post I discussed the solution to the problem "Homework" from Facebook Hacker Cup 2015 Round 1. This post is about the problem "Autocomplete" from the same round. You can  read the problem statement  available on the Facebook website. If you don't have a Facebook account, you can download problem statements from Codeforces Gym . I will re-state the problem in fewer lines. You have a new phone which has an auto-complete feature. But, it will complete your word only if there is there is no ambiguity on how the word should be completed. Formally, it will complete a word iff there is exactly one way to complete the word. It so happens that the phone's dictionary is empty by default. So, for the auto-complete feature to work, before typing a word you need to add that word to the dictionary. You need to send a message containing \(N\) words. What is the minimum number of characters must you type to send all \(N\) words? (Note that the

It's been a long time since I last wrote on this blog and a lot has happened since then. The most important of all is that my personal website is up at  anirudhrb.com  and consequently this blog can now be accessed at  blog.anirudhrb.com . Also, you can now reach through email at  mail@anirudhrb.com . Let's get down to business now. The online part of Facebook Hacker Cup 2015 concluded recently and the top 25 contestants have been selected to compete in the onsite finals. The problem I am writing about in this post appeared in the Round 1 (there were 3 rounds). The title of the problem is "Homework" and here is the abridged statement: Given three integers \(A\), \(B\) and \(K\), find the number of integers in range \(\big[A, B\big] \) that have a "primacity" of \(K\). Primacity of a number \(N\) is defined as the number of distinct prime factors of \(N\). You have to process \(T\) such queries. The constraints are as follows: \(2 \le A \le B \le 10^